MCC POR VARIABLES CENTRADAS

La típica forma de realizar MCC es mediante variables absolutas, pero existe otro método. La otra forma de encontrar los mismos valores para los parámetros b es mediante variables centradas. Una variable centrada significa centrada en su media, o sea que tomaremos la variable estándar y le restaremos su media y así obtendremos una variable centrada: .

Para ello comenzamos como si fuese MCC con las variables absolutas. Lo primero será expresar el error al cuadrado y minimizarlo (a modo de ejemplo se trabajará con dos variables explicativas):

C.P.O.   

Una vez obtenidas las condiciones de primer orden, cambiaremos el rumbo para trabajar con variables centradas. Tomaremos de las condiciones de primer orden la primera ecuación y la expresaremos de la siguiente manera:

   o sea que  .

Ahora divido ambos por n y queda:

  y despejando se obtiene  .

Ahora se introduce esta última ecuación en la segunda (I en II)

Se construyen las variables centradas (y, xi) y reemplazando la X de afuera del corchete por una centrada más su media. Después se distribuye:

Se distribuye la sumatoria[1]:

Obsérvese que la sumaria una variable centrada es cero por lo que los tres últimos términos se eliminan. Después se pasan los términos de las variables independientes al otro lado y tenemos:

Haciendo lo mismo pero con la tercera ecuación tendremos (I en III):

Con estas dos últimas ecuaciones puedo formar las matrices para variables centradas:

 

Por último, para encontrar la ordenada al origen se aplica la ecuación antes vista: .

Nótese que el método para resolver con variables centradas nos lleva a una ecuación en matrices igual a la vista antes pero con una fila y una columna menos, o sea que tendremos la ventaja de trabajar con una matriz más pequeña.

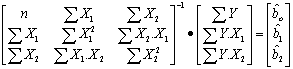(Se debe elimnar primera fila y primera columna)

 Por último debe aclararse que la forma matricial para calcular el R2 , para el T.S.G.(F), para el T.S.I.(t) u otros será la misma.

[1] A partir de aquí los signos de sumatoria dejarán de tener índice solo por comodidad.